2024年12月13日，应学校优化团队带头人彭再云邀请，韩国国立釜庆大学Do Sang Kim教授、东北师范大学矫立国、延边大学洪哲莅临我校进行学术交流与指导，并举行了“2024优化理论、算法及应用国际前沿研讨会”第二场报告。Do Sang Kim教授和矫立国老师在南岸校区二教7楼教师发展中心分别作了“无穷远处次微分及其在优化中的应用”和“非退化半代数优化中的无穷远处费马规则”的专题报告，会议由工程数学与力学研究所副所长彭再云教授主持，学院优化理论与应用团队及学校相关师生参加了会议。
会议开始，彭再云教授首先对Do Sang Kim教授、矫立国老师和洪哲老师的到来表示热烈的欢迎，并感谢专家对学院学术团队的指导和帮助。Do Sang Kim教授的报告聚焦于无穷远处的次微分及其在优化中的应用，主要贡献如下：一是定义并研究了无穷远处集合的法锥以及函数的极限和奇异次微分，给出计算规则；二是证明函数在无穷远处是Lipschitz的当且仅当其奇异次微分在无穷远处为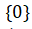
，且在此等价条件下，函数在无穷远处的Clarke次微分等于极限次微分的凸包；三是针对优化问题，在函数有下界且无解时给出无穷远处的必要最优性条件；四是在特定条件下，证明函数具有强制性、弱尖锐极小值性质及扰动优化问题解的稳定性等。最后Do Sang Kim教授阐述此理论在优化方面的应用，为优化理论与实践提供关键支撑，拓展优化问题分析视角与解决途径。
之后，由矫立国老师进行了关于非退化半代数优化中无穷远处的费马规则的报告。在无约束情形下，针对多项式函数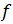
的下确界问题展开，依
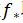取值及是否取到下确界分类探讨，引入牛顿多面体剖析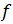与相关函数
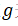关系，给出无穷远处费马规则定理。约束情形时，先明确问题
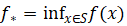，已知取到下确界的条件，对未取到下确界时探寻必要最优性条件遇阻，遂引入无穷远处锥
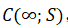，阐释其定义、性质（如与S的半代数性关联、计算关系、非平凡性判别及交并规则等）及函数在S上无穷远处非退化定义。最终得出主要定理：满足
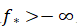且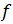在S上无穷远处非退化，若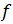未取到下确界，则
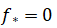或存在特定点、集合与向量使相关等式成立，且证明了无需约束规格假设，辅以实例及未来设计计算相关元素算法的研究方向。
优化国际会议系列第二场交流圆满结束，本场报告与交流为与会师生提供了交流平台、前沿研究思路，期待未来能有更多的关于优化及应用及相关方向的报告与交流，继续推动重庆交通大学数学与统计学院在向量优化领域的建设和发展。
Do Sang Kim教授简介
Do Sang Kim教授：生于1953年，毕业于韩国国立釜山大学,现为国立釜庆大学应用数学专业名誉教授，曾任研究生院院长。曾先后在意大利美国作访问学者，多年来致力于多目标最优化，广义凸分析，变分分析等方向的研究，至今累计发表Mathematical Programming, Mathematics of Operations Research, Journal of Optimization Theory and Applications等SCI论文100余篇，现担任Journal of Nonlinear and convex Analysis等学术期刊编委，期间取得众多突破性的研究成果。曾先后主持韩国BK21(21世纪Brain Korea)，BK21+(21世纪Brain Korea Program of Leading Universities &students)等团体学术项目以及韩国研究财团的个人研究项目多项。亦先后获得釜山科学技术奖,大韩数学会特别功劳奖/教育奖等多项国家级奖项，参与创办Nonlinear Analysis and Optimization和Nonlinear Analysis and convex Analysis等两个活跃于东亚的大型国际学术会议。
矫立国老师简介
矫立国：男，东北师范大学前沿交叉研究院助理研究员，硕士生导师，主要研究方向为具有半代数结构的优化理论与算法，在Comput.Optim.Appl.,J. Global Optim.,J.Optim.Theory Appl等期刊发表论文多篇，申请发明专利1项（实审阶段），目前担任J.Nonlinear Convex Anal客座主编。带领团队对接国家卫星资源中心中电科下辖多个院所、浙江大学、电子科技大学等科研院所和高校，开展联合协作，提出了一系列解决实际应用问题的新思路、新方法，得到了军事科学院等第三方的高度认可。
